回溯算法

回溯

77 组合

77. 组合

难度中等1043

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

解答

class Solution {
    public List<List<Integer>> combine(int n, int k) {
       List<List<Integer>> res=new ArrayList<>();
       if(k<=0 || n<1){
           return res;
       }
        Deque<Integer> temp=new LinkedList<>();
        int begin=1;
        backTrack(res,temp,begin,n,k);
        return  res;
    }
     public static void backTrack(List<List<Integer>> res,  Deque<Integer> temp,int begin,int n, int k) {
        if(temp.size()==k){
            res.add(new ArrayList<>(temp));
            return;
        }
        for (int i = begin; i <=n ; i++) {
            temp.add(i);
            backTrack(res,temp,i+1,n,k);
            temp.removeLast();
        }
    }
}

优化

剪枝优化

在遍历的过程中有如下代码：

for (int i = startIndex; i <= n; i++) {
    path.push_back(i);
    backtracking(n, k, i + 1);
    path.pop_back();
}

这个遍历的范围是可以剪枝优化的，怎么优化呢？

来举一个例子，n = 4，k = 4的话，那么第一层for循环的时候，从元素2开始的遍历都没有意义了。 在第二层for循环，从元素3开始的遍历都没有意义了。

这么说有点抽象，如图所示：

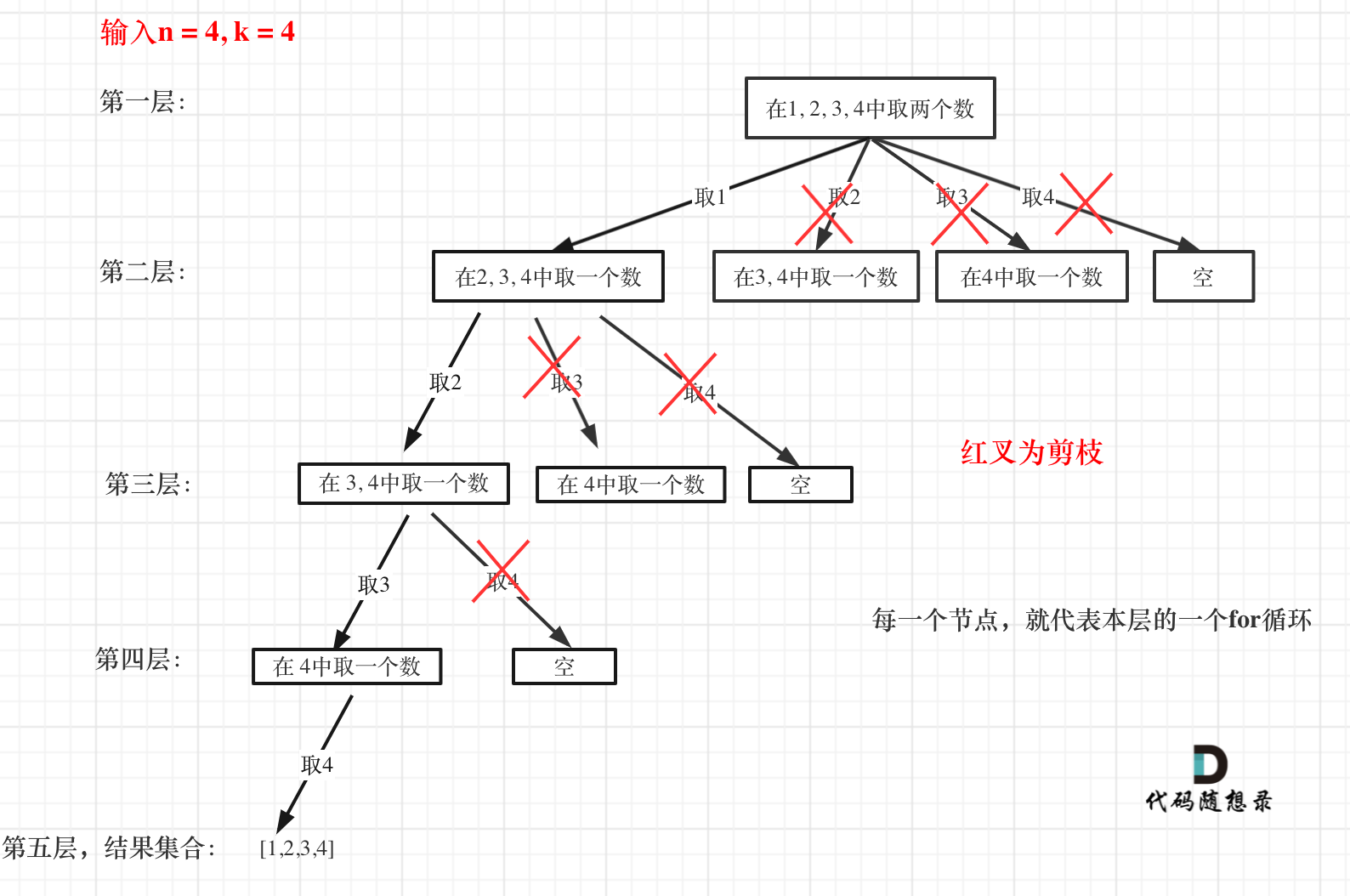
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置

216 组合总和 III

216. 组合总和 III

难度中等501

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

• 只使用数字1到9
• 每个数字 最多使用一次

返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

示例 2:

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。

示例 3:

输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字，我们可以得到的最小和是1+2+3+4 = 10，因为10 > 1，没有有效的组合。

解答

class Solution {
    public List<List<Integer>> combinationSum3(int k, int n) {
       List<List<Integer>> res=new ArrayList<>();
        Deque<Integer> temp=new LinkedList<>();
        backTrack(res,temp,1,n,k);
        return res;
    }
     private static void backTrack( List<List<Integer>> res, Deque<Integer> temp,int begin,int n,int k){
        if(temp.size()==k ){
            if(sum(temp)==n) {
                res.add(new ArrayList<>(temp));
                return;
            }else{
                return;
            }
        }
        for (int i = begin; i <=9 ; i++) {
            temp.add(i);
            backTrack(res,temp,i+1,n,k);
            temp.removeLast();
        }
    }

    public static int sum(Deque<Integer> temp){
        int sum=0;
        for (Integer integer : temp) {
            sum+=integer;
        }
        return sum;
    }
}

17 .电话号码的字母组合

17. 电话号码的字母组合

难度中等1992

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

输入：digits = ""
输出：[]

示例 3：

输入：digits = "2"
输出：["a","b","c"]

提示：

• 0 <= digits.length <= 4
• digits[i] 是范围 ['2', '9'] 的一个数字。

解答

class Solution {
    public List<String> letterCombinations(String digits) {
         List<String> res=new ArrayList<>();
         if (digits == null || digits.length() == 0) {
            return res;
        }
        
        String  [] str=new String[]{"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
        StringBuilder builder=new StringBuilder();
        backTrack(res,digits,builder,str,0);
        return res;

    }
     private static void backTrack(List<String> res, String digits,  StringBuilder builder,String[] str, int num) {
        if(num==digits.length()){
            res.add(builder.toString());
            return;
        }
        String s=str[digits.charAt(num)-'0'];
        for (int i = 0; i <s.length() ; i++) {
            builder.append(s.charAt(i));
            backTrack(res,digits,builder,str,num+1);
            builder.deleteCharAt(builder.length()-1);
        }
    }
}

39 组合总和

39. 组合总和

难度中等2053

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

提示：

1 <= candidates.length <= 30
1 <= candidates[i] <= 200
candidate 中的每个元素都 互不相同
1 <= target <= 500

解答

class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
    List<List<Integer>>  res=new ArrayList<>();
        Deque<Integer> path=new LinkedList<>();
        Arrays.sort(candidates);
        int sum=0;
        int index=0;
        backTrack(res,path,candidates,target,sum,index);
        return res;

    }

     public static void backTrack(List<List<Integer>>  res,Deque<Integer> path,int []candidates,int target,int sum,int index){
        if(sum==target) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = index; i <candidates.length ; i++) {
            if(sum+candidates[i]>target){
                break;
            }
            path.add(candidates[i]);
            backTrack(res,path,candidates,target,sum+candidates[i],i);
            path.removeLast();
        }

    }
    
}

40. 组合总和 II

40. 组合总和 II

难度中等1026

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

注意：解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]

提示:

• 1 <= candidates.length <= 100
• 1 <= candidates[i] <= 50
• 1 <= target <= 30

:dagger: 解答一(超时，但用例通过)

class Solution {
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
         List<List<Integer>>  res=new ArrayList<>();
        Deque<Integer> path=new LinkedList<>();
        Arrays.sort(candidates);
        int sum=0;
        int index=0;
        backTrack(res,path,candidates,target,sum,index);
        return res;

    }

    public static void backTrack(List<List<Integer>>  res, Deque<Integer> path, int []candidates, int target, int sum, int index){
        if(sum==target && !res.contains(path)) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = index; i <candidates.length ; i++) {
            if(sum+candidates[i]>target){
                break;
            }
            path.add(candidates[i]);
            backTrack(res,path,candidates,target,sum+candidates[i],i+1);
            path.removeLast();
        }

    }
}

解答二

class Solution {
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
         List<List<Integer>>  res=new ArrayList<>();
        Deque<Integer> path=new LinkedList<>();
        Arrays.sort(candidates);
        int sum=0;
        int index=0;
        backTrack(res,path,candidates,target,sum,index);
        return res;
    }

    public static void backTrack(List<List<Integer>>  res, Deque<Integer> path, int []candidates, int target, int sum, int index){
        if(sum==target) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = index; i <candidates.length ; i++) {
            if(i>index && candidates[i]==candidates[i-1]){
                continue;
            }
            if(sum+candidates[i]>target){
                break;
            }
            path.add(candidates[i]);
            backTrack(res,path,candidates,target,sum+candidates[i],i+1);
            path.removeLast();
        }

    }
}

131 分割回文串

131. 分割回文串

难度中等1191

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

回文串 是正着读和反着读都一样的字符串。

示例 1：

输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

示例 2：

输入：s = "a"
输出：[["a"]]

提示：

• 1 <= s.length <= 16
• s 仅由小写英文字母组成

class Solution {
    public List<List<String>> partition(String s) {
       List<List<String>> res = new ArrayList<>();
        Deque<String> path = new LinkedList<>();
        int index = 0;
        backTrack(res, path, s, index);
        return  res;
    }

     public static void backTrack(List<List<String>> res, Deque<String> path, String s, int index) {
        if (index >= s.length()) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = index; i < s.length(); i++) {
            if (checkPalindrome(s, index, i)) {
               String temp=s.substring(index,i+1);
                path.add(temp);
            }else{
                continue;
            }
            backTrack(res, path, s, i + 1);
            path.removeLast();

        }

    }


    public static boolean checkPalindrome(String s, int start, int end) {
        for (int i =start, j = end; i < j; i++, j--) {
            if (s.charAt(i) != s.charAt(j)) {
                return false;
            }
        }
        return true;

    }
}

93 复原ip地址

93. 复原 IP 地址

难度中等954

有效 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。

• 例如："0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址，但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效 IP 地址。

给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。

示例 1：

输入：s = "25525511135"
输出：["255.255.11.135","255.255.111.35"]

示例 2：

输入：s = "0000"
输出：["0.0.0.0"]

示例 3：

输入：s = "101023"
输出：["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]

提示：

• 1 <= s.length <= 20
• s 仅由数字组成

解答

注意要点：

1.判断ip是否有效

2.是针对原本字符串进行改变了

3.s=s.substring(0,i+1)+”.”+s.substring(i+1); 理解为什么要从0开始截取 而不是从startIndex

class Solution {
    public List<String> restoreIpAddresses(String s) {
    List<String> res=new ArrayList<>();
        if(s.length()>12){
            System.out.println(res);
        }
        int startIndex=0;
        int pointNum=0;
        backTrack(s,res,startIndex,pointNum);
        return res;
    }

    public static void backTrack(String s,List<String> res,int startIndex,int pointNum){
        if(pointNum==3){
            if(isValid(s,startIndex,s.length()-1)){
                res.add(s);
            }
              return;
        }

        for (int i = startIndex; i < s.length(); i++) {
            if(isValid(s,startIndex,i)){
                s=s.substring(0,i+1)+"."+s.substring(i+1);
                pointNum++;
                backTrack(s,res,i+2,pointNum);
                s=s.substring(0,i+1)+s.substring(i+2);
                pointNum--;
            }else{
                break;
            }
        }
    }

    private static boolean isValid(String s,int startIndex,int endIndex) {
        int num=0;
        if(startIndex>endIndex){
            return false;
        }
        //以0开头  且不是单位  为false
        if(s.charAt(startIndex)=='0' && startIndex!=endIndex){
            return false;
        }
        for (int i = startIndex; i <= endIndex; i++) {
            if(s.charAt(i)<'0' || s.charAt(i)>'9'){
                return false;
            }
            num=num*10+s.charAt(i)-'0';
            if(num>255){
                return false;
            }

        }
        return true;

    }
}

78 子集

78. 子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

• 1 <= nums.length <= 10
• -10 <= nums[i] <= 10
• nums 中的所有元素 互不相同

解答

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> res=new ArrayList<>();
        Deque<Integer> path=new LinkedList<>();
        int begin=0;
        backTrack(res,path,begin,nums);
        return  res;
    }

     public static void backTrack(List<List<Integer>> res,Deque<Integer> path,int begin,int []nums){
        res.add(new ArrayList<>(path));
        for (int i = begin; i <nums.length ; i++) {
            path.add(nums[i]);
            backTrack(res,path,i+1,nums);
            path.removeLast();
        }
    }
}

90 子集②

90. 子集 II

难度中等874

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

示例 1：

输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

解答:

class Solution {
    public List<List<Integer>> subsetsWithDup(int[] nums) {
       List<List<Integer>> res=new ArrayList<>();
        Deque<Integer> path=new LinkedList<>();
        int begin=0;
        Arrays.sort(nums);
        backTrack(res,path,begin,nums);
        return  res;
    }

     public static void backTrack(List<List<Integer>> res, Deque<Integer> path,int begin,int []nums){
        res.add(new ArrayList<>(path));
        for (int i = begin; i <nums.length ; i++) {
            if(i>begin && nums[i]==nums[i-1]){
                continue;
            }
            path.add(nums[i]);
            backTrack(res,path,i+1,nums);
            path.removeLast();
        }
    }
}

491 递增子序列

491. 递增子序列

难度中等471

给你一个整数数组 nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。

数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。

示例 1：

输入：nums = [4,6,7,7]
输出：[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]

示例 2：

输入：nums = [4,4,3,2,1]
输出：[[4,4]]

提示：

• 1 <= nums.length <= 15
• -100 <= nums[i] <= 100

解答 （用模板套 不好做出来）

class Solution {
    public List<List<Integer>> findSubsequences(int[] nums) {
       List<List<Integer>> res=new ArrayList<>();
        Deque<Integer> path=new LinkedList<>();
        int begin=0;
        backTrack(res,path,begin,nums);
        return res;
    }

     private static void backTrack(List<List<Integer>> res, Deque<Integer> path, int begin, int[] nums) {
        if(path.size()>=2){
            res.add(new ArrayList<>(path));
        }
        int[] used = new int[201];
        for (int i = begin; i <nums.length ; i++) {
            if(!path.isEmpty() && nums[i]<path.getLast() || used[nums[i]+100]==1)
            {
                continue;
            }
            used[nums[i]+100]=1;
            path.add(nums[i]);
            backTrack(res,path,i+1,nums);
            path.removeLast();

        }

    }
}

46 全排列

46. 全排列

难度中等2104

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

• 1 <= nums.length <= 6
• -10 <= nums[i] <= 10
• nums 中的所有整数 互不相同

解答

跟以往不一样的是 for（int i=0;i<nums.length;i++）

而以往是 for（int i=begin;i<nums.length;i++）因为排列问题，每次都要从头开始搜索，例如元素1在[1,2]中已经使用过了，但是在[2,1]中还要再使用一次1。

class Solution {
    public List<List<Integer>> permute(int[] nums) {
       boolean []used=new boolean[nums.length];
        List<List<Integer>>  res=new ArrayList<>();
        Deque<Integer>  path=new LinkedList<>();
        int begin=0;
        backTrack(res,path,used,begin,nums);
        return  res;
    }
    private static void backTrack(List<List<Integer>> res, Deque<Integer> path, boolean[] used, int begin, int[] nums) {
     if(path.size()==nums.length){
         res.add(new ArrayList<>(path));
         return;
     }
        for (int i = 0; i <nums.length ; i++) {
            if(used[i]){
               continue;
            }
            used[i]=true;
            path.add(nums[i]);
            backTrack(res,path,used,i+1,nums);
            used[i]=false;
            path.removeLast();
        }
   }
}

47 全排列2

47. 全排列 II

难度中等1120

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
[1,2,1],
[2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

• 1 <= nums.length <= 8
• -10 <= nums[i] <= 10

解答

class Solution {
    public List<List<Integer>> permuteUnique(int[] nums) {
       boolean []used=new boolean[nums.length];
        List<List<Integer>>  res=new ArrayList<>();
        Arrays.sort(nums);
        Deque<Integer>  path=new LinkedList<>();
        int begin=0;
        backTrack(res,path,used,begin,nums);
        return  res;
    }
    private static void backTrack(List<List<Integer>> res, Deque<Integer> path, boolean[] used, int begin, int[] nums) {
     if(path.size()==nums.length){
         res.add(new ArrayList<>(path));
         return;
     }
        for (int i = 0; i <nums.length ; i++) {
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                continue;
            }
            if(used[i]==false){
            used[i]=true;
            path.add(nums[i]);
            backTrack(res,path,used,i+1,nums);
            used[i]=false;
            path.removeLast();
            }
        }
   
    }
}